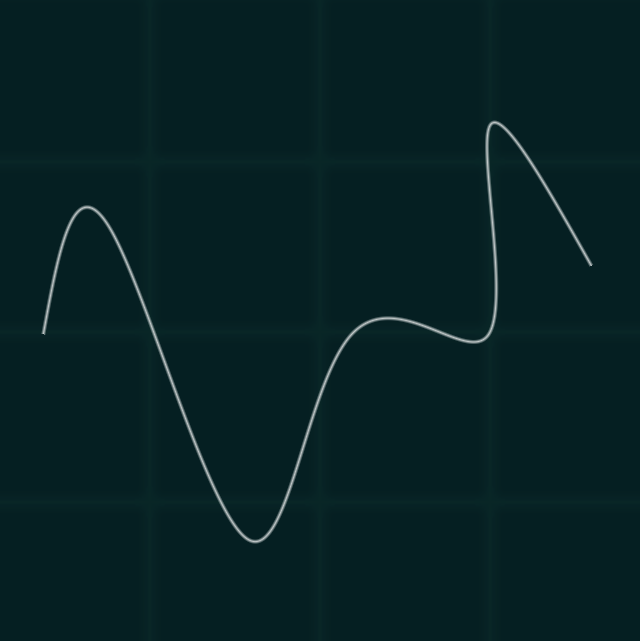
Curves

Bezier Curve

A Bézier curve is a parametric curve defined by control points, often used in computer graphics and modeling. It follows polynomial functions of varying degrees, typically cubic or quadratic, allowing smooth curve manipulation. The shape and trajectory of the curve are determined by the positions of its control points, enabling precise and versatile curve generation in graphical applications and design software.

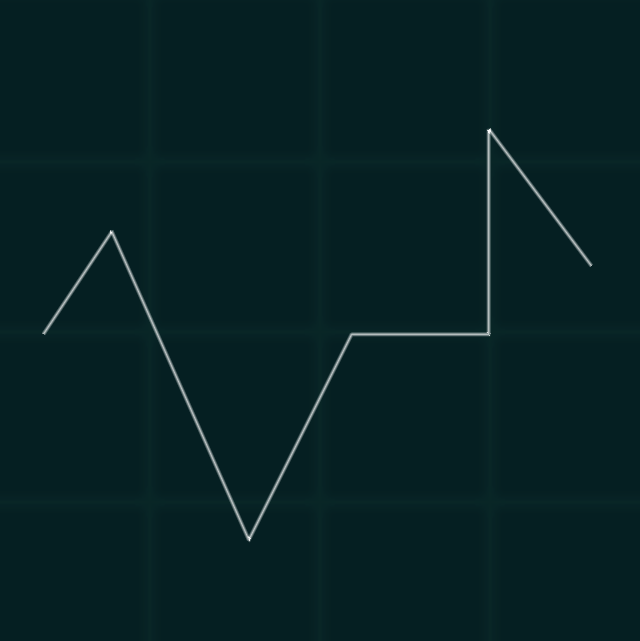
Linear Spline

A linear spline is a piecewise-linear function composed of several connected line segments. It's used in interpolation and approximation, employing straight lines between given points to create a continuous curve. Each segment connects adjacent points, ensuring smoothness and continuity at these junctions. Linear splines serve as simple yet effective tools in various mathematical and computational fields due to their simplicity and predictability. A closed linear spline (i.e, the first point and the last are the same) in the plane is just a polygon.

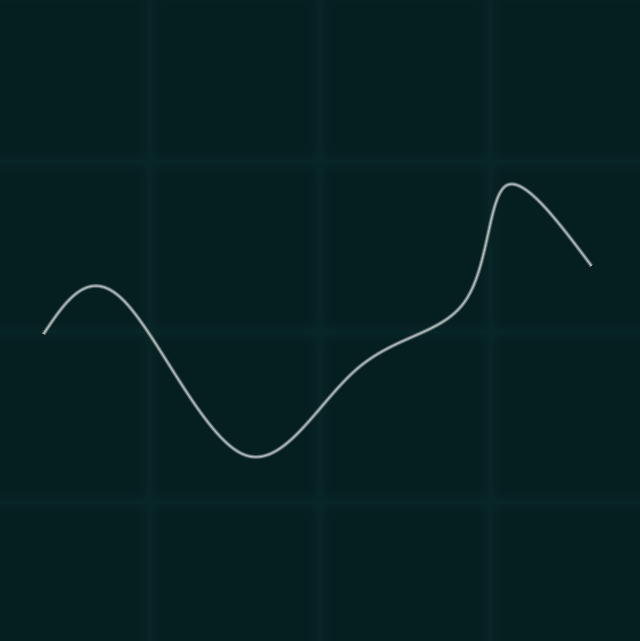
BSpline

A B-spline is a mathematical curve defined by blending together polynomial functions through control points and knot vectors. Named after its basis functions, B-splines maintain local control through these control points, allowing flexible manipulation of the curve's shape without affecting distant segments. Their versatility in representing complex shapes and smoothness across transitions finds applications in computer graphics, CAD, and curve fitting.

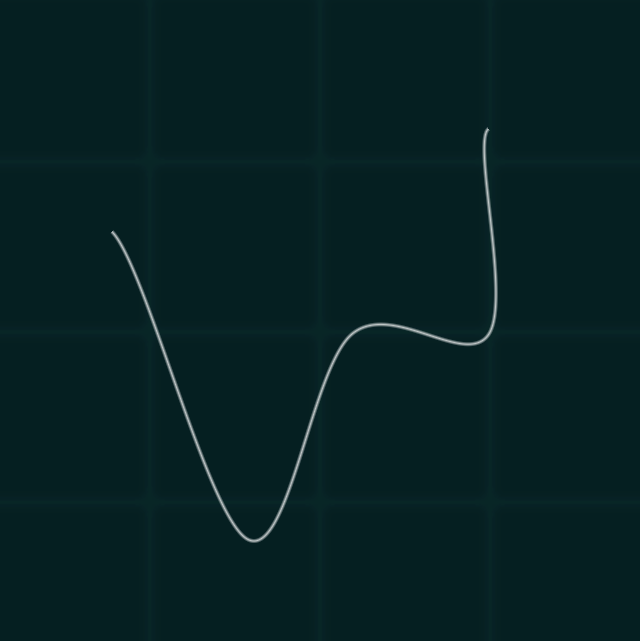
Catmull-Rom

A Catmull-Rom spline is a type of interpolating spline used in computer graphics and geometric modeling. It ensures a smooth curve passing through given control points by calculating each segment's path based on neighboring points. Known for maintaining local control and generating continuous, tangent-connected curves, Catmull-Rom splines avoid overshooting and exhibit predictable behavior, making them valuable in animation and design applications.

Cubic Spline

A cubic spline is a piecewise-defined curve composed of cubic polynomial segments. Defined by given points, it ensures a smooth and continuous curve with connected segments featuring second-order continuity. By employing polynomials of degree three, cubic splines offer flexibility in approximating various functions and data sets. Widely used in interpolation, curve fitting, and numerical analysis, they provide an effective method for approximating complex relationships between data points.